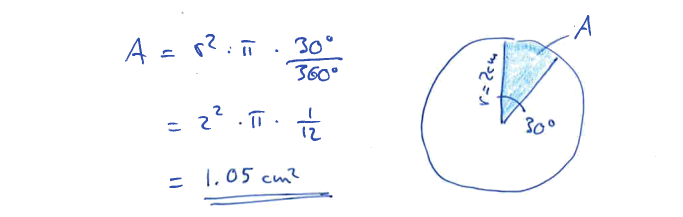Kreis
Kreisumfang
Jeder Kreis besitzt ein einbeschriebenes und ein umbeschriebenes Vieleck. Je grösser die Anzahl der Ecken der Vielecke ist, desto mehr nähern sich ihre Umfänge dem Umfang des Kreises. Der genaue Wert liegt zwischen dem Umfang des einbeschriebenen und dem Umfang des umbeschriebenen Vielecks. Ein Kreis kann als ein Vieleck mit unendlich grosser Anzahl Ecken angesehen werden.

Die Zahl, die angibt, wie oft der Durchmesser eines Kreises im Umfang enthalten ist, nennt man π (Pi) = 3.1415926.. Für die Rechnung genügt in den meisten Fällen der Wert π = 3.14
Der Kreis mit dem Durchmesser d oder dem Radius r hat den Umfang
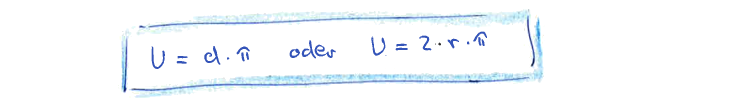
Beispiel: Der Äquator hat eine Länge von 40'000 km. Wie lang ist der Radius der Erde?

Kreisfläche
Um den Flächeninhalt des Kreises zu berechnen, denkt man sich den Kreis in viele kleine Dreiecke zerlegt, die man zu einer rechteckähnlichen Figur zusammensetzen kann. Vergrössert man die Anzahl der Dreiecke, so geht die Figur immer mehr in ein Rechteck über. Alle Dreiecksgrundseiten zusammen ergeben den Kreisumfang (2rπ). Die Seiten des Rechtecks sind also der Halbmesser r und der halbe Kreisumfang rπ.

Der Flächeninhalt des Kreises ist daher

Also hat der Kreis mit dem Radius r oder dem Durchmesser d den Flächeninhalt
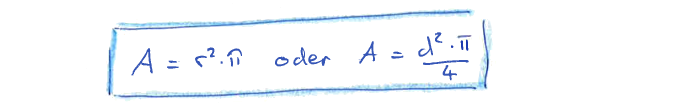
Beispiel: Ein kreisrunder Platz hat einen Durchmesser von 46 m. In seiner Mitte befindet sich eine Verkehrsinsel von 9.5 m Durchmesser. Wie viel m2 bleiben für den Verkehr übrig?

Kreisbogen
Die Länge des Kreisbogens zum Mittelpunktswinkel α ist:

Wird der Kreisbogen nicht als Winkel, sonder als Teil des Kreises angegeben, so ändert sich der Ansatz entsprechend.
Beispiel: Berechne die Länge eines Viertelkreises mit 2 cm Durchmesser
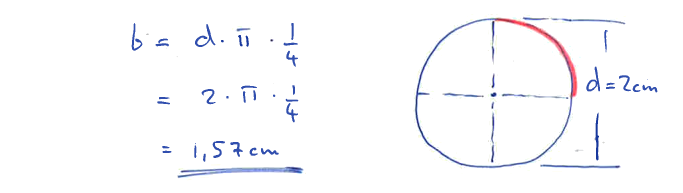
Kreisausschnitt
Analog zum Kreisbogen setzen wir an:

Beispiel: Berechne die Fläche eines Kreisauschnitts mit dem Mittelpunktswinkel 30° und 2 cm Radius.